Wielkości fizyczne, jednostki i pomiary

Poznając świat, nie tylko chcemy się dowiedzieć, jak i dlaczego coś się dzieje, ale zależy nam również na tym, aby opisywać zjawiska w sposób ilościowy, czyli za pomocą liczb. Na przykład jesli chcemy skonstrułować stolik ze szklanym blatem, to oprócz tego, że szyba pęknie pod naciskiem, warto wiedzieć np.:

ile kilogramów można na niej postawić, zanim pęknie,
jaką musi mieć grubość, aby nie pękła.

W tym celu wykonuje się pomiary.

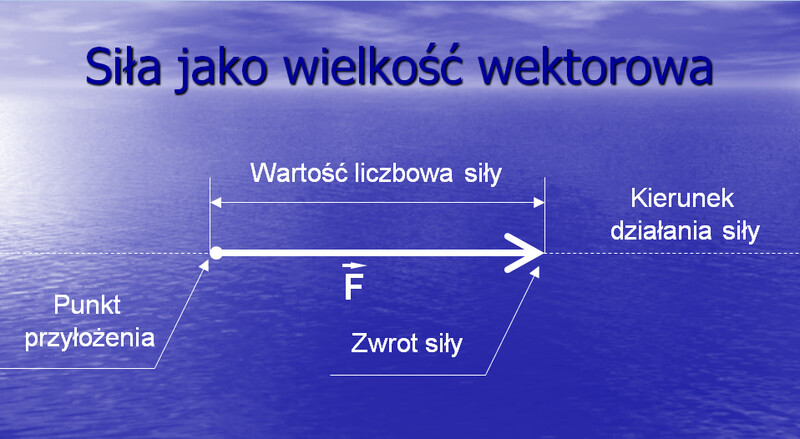
Badając cechy i właściwość ciała fizycznego, np. stalowej szyny, możemy zmierzyć jego długość, temperaturę, masę itp. Te dające się wyrazić w sposób ilościowy cechy ciała lub zjawiska nazywa się wielkościami fizycznymi. Wielkość fizyczna może przyjmować różne wartości. Wyraża się je za pomocą liczby oraz odpowiedniej jednostki, np. metrów w przypadku długości, stopni Celsjusza w przypadku temperatury, kilogramów w przypadku masy.

Jednostki układu SI.
Wielkości fizyczne wyrażamy w różnych jednostkach, np. czas podajemy w sekundach, godzinach albo latach. W niektórych krajach długość podaje się w calach albo milach, a temperaturę w stopniach Fahrenheita. Aby uporządkować sposób, w jaki opisywane są różne wielkości, wprowadzono układ SI, czyli Międzynarodowy Układ Jednostek Miar.

Poznaliśmy pięć z siedmiu podstawowych wielkości fizycznych, jednostki i urządzenia do ich pomiarów.

Praca domowa: 1, 2 i 3 str. 16

Przedrostki tworzące nazwy jednostek:

Nazwa przedrostka	Symbol	Wartość (mnożnik)
peta	P	10¹⁵ = 1 000 000 000 000 000
tera	T	10¹² = 1 000 000 000 000
giga	G	10⁹= 1 000 000 000
mega	M	10⁶= 1 000 000
kilo	k	10³= 1 000
hekto	h	10²= 1 00
deka	da	10¹= 1 0
decy	d	10^-1= 0,1
centy	c	10^-2= 0,01
mili	m	10^-3= 0,001
mikro	μ	10^-6= 0,000 001
nano	n	10^-9= 0,000 000 001
piko	p	10^-12= 0,000 000 000 001

Siła i jej cechy

Siła jest miarą oddziaływania ciał, charakteryzującą się czterema cechami: wartością, kierunkiem, zwrotem i punktem przyłożenia - jest to wielkość wektorowa.

Siłę będziemy oznaczali dużą literą F od ang. force. Dla rozróżnienia poszczególnych sił będziemy stosowali indeksy dolne przy literze F. Jednostką siły jest niuton (1N).

Siła wypadkowa i równoważąca

Wektor wypadkowy znajdujemy w następujący sposób: Do końca pierwszego dokładamy początek drugiego wektora. Następnie do końca drugiego wektora dokładamy początek trzeciego itd. Wektor wypadkowy otrzymujemy łącząc początek pierwszego z końcem ostatniego.

Powtórzenie.

Pierwsze spotkanie z fizyką

Fizyka

to nauka badająca podstawowe prawa przyrody, zjawiska w niej zachodzące oraz właściwości materii. Podstawowymi metodami badawczymi stosowanymi w naukach przyrodniczych są obserwacje i eksperymenty.

Pomiar

polega na porównaniu wartości mierzonej wielkości z wzorcem. Żaden pomiar nie jest idealnie dokładny. W poprawnie zapisanym wyniku najniższy rząd miepewności pomiarowej musi być taki sam jak najniższy rząd wartości zmierzonej.

Ciało fizyczne

Każdy przedmiot lub organizm żywy, mogący stanowić obiekt badań fizyki, to ciało fizyczne. Materiał, z którego zbudowane jest ciało fizyczne, to substancja.

Jednostka siły

Miarą oddziaływań jest siła. Siła jest wielkością wektorową. Jednostką siły jest niuton (1N).

Rodzaje oddziaływań

Można wskazać różne rodzaje oddziaływań, np.: grawitacyjne, elektrostatyczne, magnetyczne, mechaniczne.

Wielkości skalarne

Wyróżnia się wielkości skalarne (liczbowe mające wartość) i wielkości wektorowe mające wartość, kierunek, zwrot a w przypadku siły również i punkt przyłożenia.

Wielkości fizyczne

Cecha ciała lub zjawiska, którą można wyrazić liczbowo, to wielkość fizyczna. Wartości wielkości fizycznych należy zapisywać wraz z jednostkami. Jednostki główne różnych wielkości zebrano w układzie SI.

Kierunek siły

to linia prosta, wzdłuż której działa siła.

Zwrot

jest wskazany przez grot symbolu wektora.

Wartość

siły na rysunku jest odzwierciedlana za pomocą długości strzałek. Wartość siły można wyznaczyć za pomocą siłomierza.

Punkt przyłożenia

jest miejscem, w którym siła działa na ciało.

Atomy i cząsteczki

Atom to podstawowy składnik materii, którego nie da się podzielić w wyniku reakcji chemicznych. Atomy łączą się ze sobą tworząc cząsteczki różnych substancji.

Dyfuzja to samorzutne rozprzestrzenianie się cząsteczek jednej substancji w drugiej. W wyniku dyfuzji następuje mieszanie się różnych substancji.

Hipoteza o molekularnej budowie ciał:

wszystkie ciała zbudowane są z cząsteczek (molekuł);
cząsteczki są w ciągłym i chaotycznym ruchu;
cząsteczki mogą oddziaływać między sobą, mogą się zderzać, przyciągać lub odpychać.

Wszystkie powyższe hipotezy są poparte doświadczeniami, odpowiednio: kontrreakcją, dyfuzją i ruchami Browna.

Oddziaływania międzycząsteczkowe

Siły spójności odpowiadają za wzajemne przyciąganie się cząsteczek tej samej substancji.

Siły przylegania powodują wzajemne przyciąganie się cząsteczek różnych substancji.

Napięcie powierzczniowe to zjawisko powstawania cienkiej „błony” na powierzchni cieczy.

Tworzenie się kropli wody jest skutkiem występowania napięcia powierzchniowego, będącego rezultatem działania siły spójności.

Badanie napięcia powierzchniowego

Napięcie powierzchniowe zależy od różnych czynników. Oznacza to, że siły spójności działające między cząsteczkami cieczy można zmniejszyć np. poprzez podgrzewanie cieczy lub dolanie detergentu do niej.

Siły spójności działające na cząsteczki wewnątrz cieczy się równoważą.
Siły spójności działające na cząsteczki przy powierzchni cieczy nie równoważą się, dlatego powierzchnia cieczy zachowuje się jak naprężona błona.
Im większe są siły przylegania między cieczą a podłożem, tym kropla jest bardziej spłaszczona.

Stany skupienia

Trzy stany skupienia substancji
Ciało fizyczne zbudowane z danej substancji znajduje się w jednym z trzech stanów skupienia:

stanie stałym,
stanie ciekłym,
stanie gazowym, (lotnym).

Właściwości ciał stałych, cieczy i gazów
Ciała stałe mają określony kształt i określoną objętość. Kształt niektórych ciał stałych można łatwo zmienić.
Ciecze mają swoją objętość, ale nie mają swojego kształtu - przyjmują kształt naczynia, w którym się znajdują. Są mało ściśliwe.
Gazy są ściśliwe i rozprężliwe, nie mają swojego kształtu ani określonej objętości, samorzutnie wypełniają dostępną przestrzeń.

Masa a siła ciężkości

Masa ciała jest wielkością liczbową, a ciężar - wielkością wektorową.

F_g = m • g

Jednostką ciężaru (siły ciężkości) w układzie SI jest niuton – N. Symbole wielkości fizycznych, pochodzą od pierwszych liter oznaczających poszczególne wielkości fizyczne: Force, mass, gravitation.

Siła ciężkości, siła grawitacji i ciężar to słowa synonimy. Dla uproszczenia w szkole podstawowej na lekcjach fizyki będzie oznaczać to samo. Będziemy używać tych słów zamienne. W szkole średniej dowiesz się o konkretnym ich znaczeniu (nie koniecznie oznaczają to samo).

Zadanie 5/73 (podręcznik)

Oblicz ciężar skrzynki jabłek o masie 10,4 kg.

Zadanie 6/73 (podręcznik)

Robert częściowo uzupełnił tabelę, w której wpisał wyniki obliczonych mas przedmiotów, gdy podany był ich ciężar.

Przedmiot	Samochód osobowy	Plecak z książkami	Zeszyt	Rower	Kalkulator
Ciężar [N]	9000	50	1,8	160	0,8
Masa [kg]	900	5

Przerysuj powyższą tabelkę do zeszytu, następnie zapisz w zeszycie, ile wynoszą masy: zeszytu, roweru oraz kalkulatora. Opisz sposób obliczania masy w kilogramach, gdy znany jest ciężar w niutonach.

Gęstość

Gęstość to liczbowa wielkość fizyczna charakterystyczna dla danej substancji, określająca masę tej substancji zawartą w jednostkowej objętości.

d	=	m
		V

d	-	gęstość;
m	-	masa;
V	-	objętość;

Jednostką gęstości w układzie SI jest kg/m³. Co to znaczy, że gęstość substancji wynosi 1000 kg/m³? Wyobraż sobie sześcian o wymiarach: 1 m × 1 m × 1 m, który ma masę równą 1000 kg. Jest on wykonany z materiału o gęstości 1000 kg/m³.

Na rysunku powyżej znajdują się w cylindrze miarowym niemieszane ze sobą ciecze o różnej gęstości. „Lżejsze” czyli te o mniejszej gęstości są na górze. Ciecze zostały dodatkowo zabarwione farbą spożywczą w celu lepszego kontrastu.

Zadanie 5/77 (podręcznik)

Oblicz objętość płyty styropianu o gęstości 20 kg/m³ i masie 0,25kg. Wyraź tę objętość w m³ oraz dm³.

Kładziemy drewniany klocek na trzech ściankach o różnych powierzchniach. — Kładziemy drewniany klocek na trzech ściankach o różnych powierzchniach

Ślad jest najgłębszy, gdy klocek jest ustawiony na najmniejszej ściance

Siła nacisku na podłoże. Parcie i ciśnienie

Na zdjęciach obok widzimy ślady pozostawione w mące po drewnianym klocku. Ślad jest najgłębszy, gdy pudełko jest ustawione na najmniejszej ściance, a najpłytszy, gdy stoi na największej.

Nacisk pudełka na mąkę w każdym wypadku jest taki sam - jest równy co do wartości ciężarowi pudełka. Widzimy jednak, że w zależności od ustawienia pudełka, a więc od pola powierzchni, na którą działa siła nacisku, skutki są różne.

Nacisk to składowa siły, z jaką jedno ciało działa na powierzchnię drugiego. Siła nacisku jest zawsze prostopadła do powierzchni, na którą działa.

p	=	F_n
		S

p	-	ciśnienie (od ang. pressure);
F_n	-	wartość siły nacisku (od ang. Force);
S	-	pole powierzchni (od ang. Surface);

Jeden paskal (1 Pa) jest to ciśnienie, jakie wywiera siła nacisku na pole powierzchni 1 m².

Nazwę jednostki „paskal” ustalono, aby upamiętnić zasługi wielkiego francuskiego fizyka Blaise’a Pascala, który żył w latach 1623-1662. Był on wybitnym matematykiem, fizykiem, filozofem i pisarzem. Prowadził badania nie tylko nad ciśnieniem, opracował również wiele teorii matematycznych, w tym teorię prawdopodobieństwa. Skonstruował też pierwszą na świecie maszynę liczącą (sumującą).

Często używane są wielokrotności paskala: hektopaskal (1 hPa = 100 Pa), kilopaskal (1 kPa = 1000 Pa), megapaskal (1 MPa = 1 000 000 Pa).

Zadanie 1 (Podręcznik strona 93)

Wyraź w paskalach:

a. 1020 hPa, b. 0,1 kPa, c. 0,002 MPa,

Zadanie 2 (Podręcznik strona 93)

Jeden z producentów huśtawek dla dzieci podaje, że jego produkt wytrzymuje ciśnienie 2222 Pa. Oblicz powierzchnię siedziska huśtawki, jeżeli można na niej bezpiecznie posadzić dziecko o masie maksymalnie 20 kg.

Ciśnienie hydrostatyczne, ciśnienie atmosferyczne

Patrząc na rysunek obok, możemy zaobserwować, że: Na dole butelki musi panować największe ciśnienie, ponieważ woda wylatuje z niej najdalej. Następnie dochodzimy do wniosku, że ciśnienie hydrostatyczne zależy od głębokości wody. Wysokości słupa cieczy hight.

p	-	ciśnienie;
d	-	gęstość;
g	-	przyspieszenie ziemskie;
h	-	wysokość słupa cieczy;

Ciśnienie wywierane przez słup cieczy nazywa się ciśnieniem hydrostatycznym. Rośnie ono wraz z wysokością słupa cieczy i jej gęstością. Ciśnienie atmosferyczne to ciśnienie, jakie wywiera powietrze na Ziemię i wszystkie ciała znajdujące się w atmosferze Ziemskiej. Im wyżej nad powierzchnią Ziemi, tym ciśnienie powietrza jest niższe.

Zadanie

Wymień nazwy przyrządów, za pomocą których można zmierzyć ciśnienie.
Podaj nazwę jednostki ciśnienia z układu SI obecnie stosowaną w Polsce, oraz kilka innych które btły wcześniej stosowane.

Ciśnienie hydrostatyczne - rozwiązywanie zadań

Przykłady zadań:

U podstawy tamy panuje ciśnienie hydrostatyczne równe 0,2 MPa. Oblicz wysokość tamy.

Wykonaj jeszcze raz obliczenia dla innego ciśnienia

Niektóre zegarki wodoodporne wytrzymują ciśnienie 2,06 MPa. Oblicz głębokość, na jaką może zejść nurek z takim zegarkiem na ręku, aby zegarek nie uległ zniszczeniu. Przyjmij, że gęstość wody morskiej wynosi 1030 kg/m³ a ciśnienie atmosferyczne wynosi 1013 hPa.

Przeanalizuj jeszcze raz zadanie dla innych danych, tzn. wpisz inne ciśnienia.

W naczyniu o wysokości 20 cm znajduje się pewna ciecz. Wywiera ona na dno naczynia ciśnienie hydrostatyczne 1840 Pa. Jaka to może być ciecz? Skorzystaj z tabeli na stronie 274 (podręcznik).

Prawo Pascala

Ciecze i gazy mają szczególne cechę: przenoszą działające na nie siły jednakowo we wszystkie strony. Możemy się o tym przekonać, patrząc na ilustrację obok. Woda wytryskuje ze wszystkich otworów z jednakową prędkością.

Nacisk wywierany z zewnątrz na ciecz lub gaz powoduje jednakowy wzrost ciśnienia w całej objętości cieczy lub gazu

Zapamiętaj:

Prawo Pascala: Nacisk wywierany z zewnątrz na ciecz lub gaz powoduje jednakowy wzrost ciśnienia w całej objętości cieczy lub gazu.
Prawo Pascala wykorzystuje się np. w konstrukcji prasy hydraulicznej czyli hamulców hydraulicznych.

Zadanie

Podnośnik samochodowy może działać na zasadzie prasy hydraulicznej. Przyjmij, że mniejszy tłok ma powierzchnię 0,2 m², a większy - podnoszący samochód - ma powierzchnię 6 m². Oblicz masę przedmiotu, który położony na małym tłoku, pozwoli uzyskać równowagę. Zakładamy, że na dużym tłoku stoi samochód o masie 900kg.

Rozwiązanie zadania:

Prawo Archimedesa

Na ciało o jednakowej objętości całkowicie zanurzone w tej samej cieczy działa taka sama siła wyporu.
Na każde ciało zanurzone w cieczy działa siła wyporu zwrócona ku górze i co do wartości równa ciężarowi wypartej cieczy.
Im większa gęstość cieczy, tym większa siła wyporu działa na ciało w niej zanurzo

F_w = d_c • V_c • g

Powyżej znajduje się wzór na siłę wyporu. Symbole w nim oznaczają odpowiednio F_w – siła wyporu, d_c – gęstość cieczy, V_c – objętość ciała zanurzonego w cieczy lub inaczej objętość wypartej cieczy, g – przyspieszenie ziemskie.

Z matematycznego punktu widzenia można by zdefiniować powyższą zasadę w następujący sposób: Siła wyporu jest wprost proporcjonalna do iloczynu przyspieszenia ziemskiego, gęstości cieczy oraz objętości ciała znajdującego się pod wodą.

Ruch i jego względność

Wybrane ciało lub układ ciał, względem którego określa się położenie i ruch opisywanego ciała, nazywa się układem odniesienia
Ruch to zjawisko polegające na zmianie położenia ciała względem wybranego układu odniesienia
Tor ruchu to linia zakreślana przez poruszające się ciało. Długość toru ruchu to droga.

Ciało jest w ruchu, jeżeli zmienia swoje położenie względem wybranego układu odniesienia. To samo ciało względem jednego układu odniesienia może być w ruchu, a względem innego może być w spoczynku. Tę cechę określa się jako względność ruchu.

Położenie ciała w danej chwili można określić, stosując jedno-, dwu- lub trójwymiarowy układ współrzędnych.

Ruch jednostajny prostoliniowy

Ruch, w którym w jednakowych przedziałach czasu ciało pokonuje jednakowe odcinki drogi, to ruch jednostajny.
Prędkość w ruchu jednostajnym ma stałą wartość.
Wprost proporcjonalna zależność dwóch wielkości oznacza, że jeśli jedna z nich wzrasta, to druga również wzrasta tyle samo razy, jeśli jedna maleje, to druga maleje tyle samo razy.

Ruch jednostajny prostoliniowy to ruch, w którym ciało pokonuje jednakowe odcinki drogi w takich samych odstępach czasu, a torem jest linia prosta.

Prędkość jest wielkością wektorową. Jednostką prędkości w układzie SI jest m/s.

W ruchu jednostajnym (zarówno prostoliniowym, jak i krzywoliniowym) wartość prędkości jest stała.

Wartość prędkości w ruchu jednostajnym prostoliniowym można obliczyć ze wzoru v = s/t, gdzie s - droga, t - czas.

v	=	s
		t

v	-	wartość prędkości, czyli szybkość;
s	-	droga;
t	-	czas trwania tych drgań;

Zadanie 1/133

Wyraź wartości prędkości w podanych jednostkach.

a. 120 km/h w m/s b. 40 m/s w km/h c. 0,6 km/h w m/s b. 5 m/s w km/h

Zadanie 2/133

Oblicz drogę, jaką przebędzie samochód w ciągu 15 minut, jeżeli porusza się ze stałą prędkością 60 km/h. Rozwiązanie zapisz w zeszycie.

Zadanie 3/133

Oblicz prędkość samochodu, który jadąc ruchem jednostajnym, w ciągu 2 godzin przebył drogę 140 km.

Ruch prostoliniowy zmienny

Ruch niejednostajny jest ruchem, podczas którego prędkość ciała zmienia swoją wartość w miarę upływu czasu.
Prędkość chwilowa to prędkość ciała w danej chwili, a prędkość średnia to iloraz drogi i czasu trwania ruchu.

W ruchu prostoliniowym jednostajnie przyspieszonym i jednostajnie opóźnionym tor jest linią prostą, a przyspieszenie ma stałą wartość.
Przyspieszenie jest ielkością wektorową. Wartość przyspieszenia to iloraz zmiany prędkości i przedziału czasu, w którym ta zmiana nastąpiła:

a = Δυ/Δt. Δυ - oznacza przyrost prędkości Δt - odpowiednio oznacza czas, w którym nastąpił przyrost prędkości

Jednostką przyspieszenia jest m/s².

Zadanie 4/140

Oblicz przyspieszenie geparda, który w ciągu 2 sekund zwiększył swoją prędkość o 70 km/h.

Reguła liczb nieparzystych

Reguła dotyczy ruchu jednostajnie przyspieszonego, bez prędkości początkowej. Tzn., że na początku ciało „spoczywało”, następnie zaczęło się rozpędzać ze stałym przyspieszeniem.

Reguła liczb nieparzystych mówi nam o tym, że kolejne drogi mamy na myśli kolejne odcinki w kolejnych sekundach układają się jak liczby nieparzyste.

Na zdjęciu powyżej narysowany jest samochód z którego co 1 sekundę spada kropla oleju. Samochód rusza ze stałym przyspieszeniem a krople na drodze układają się w kolejne liczby nieparzyste.

Przykład

W 4 sekundzie ruchu jednostajnie przyspieszonego, bez prędkości początkowej ciało przebyło 21m. Oblicz drogę przebytą przez to ciało:

w 3 sekundzie; 21m:7 = 3m 5 · 3m = 15m
po 4 sekundach; 16 · 3m = 48 m
w 5 sekundzie; 9 · 3m = 27 m
po 6 sekundach. 36 · 3 m = 108 m

Zadanie 1

Po 4s ruchu jednostajnie przyspieszonego bez prędkości początkowej ciało przebyło 2m. Oblicz drogę przebytą przez ciało:

Zadanie 2

Zadanie 3

Samochód rusza ze skrzyżowania ruchem jednostajnie przyspieszonym. Po 5s przejechał 50m. Oblicz jaką drogę przejedzie:

po 7s,
w 4s,
po 3s,
w 3s.

Mąkolice 2024/2025

Fizyka - klasa 7

Fizyka 7